- شرکت مهندسی دلتا سیستم توس
- تهران: 02176490358 - 09120613870
- مشهد: 05138554285 - 09155177027
- info@persiancode.net
حذف نویز و اصلاح تصویر و تابع gaussian در متلب
آموزش پردازش تصویر و برنامه نویسی در متلب 11
می خوانیم :
1- فرمول پایه اصلاح تصویر
2- نویز متناوب با فرکانس معلوم
3-انواع فیلترهای مکانی
4-طریقه کد نویسی فیلترها در متلب
5- پیاده سازی فیلترها روی تصاویر
6- روش های متفاوت نویز گیری
حذف نویز و اصلاح تصویر و تابع gaussian و باز یابی تصویر از کار کرد های پردازش تصویر متلب میباشد .
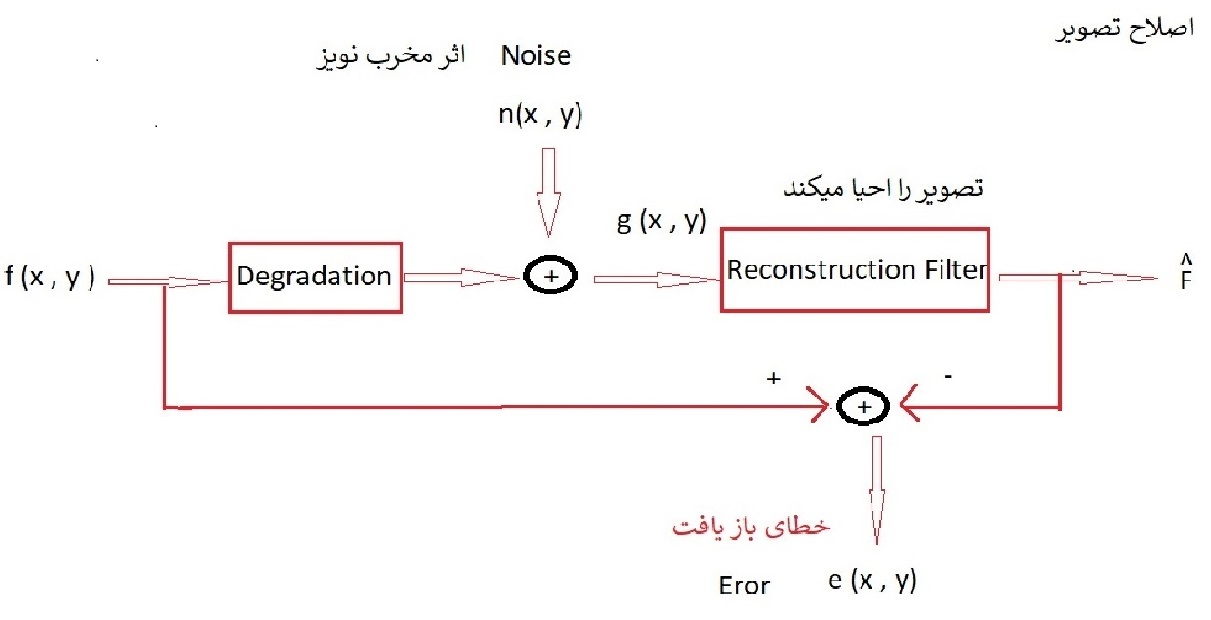
با فرمول پایه به اصلاح تصویر می پردازیم که این خود روش هایی دارد :
در مسیر مراحل اصلاح از تصویر نویز دار و خراب g به تصویر احیا شده f^ میرسیم .
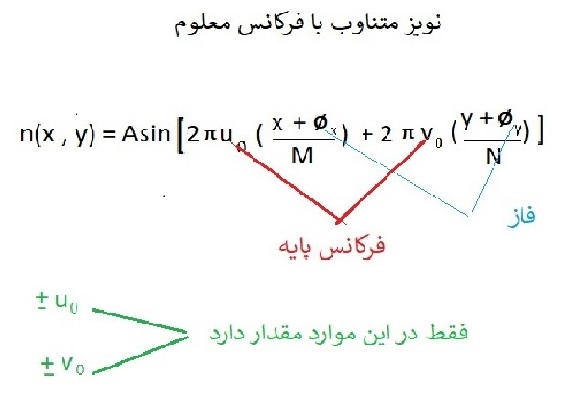
یک نویز متناوب با یک فرکانس معلوم ساده ترین حالت آن است ، چون N , H مجهول است پیدا کردن دقیق خطا ممکن نیست .
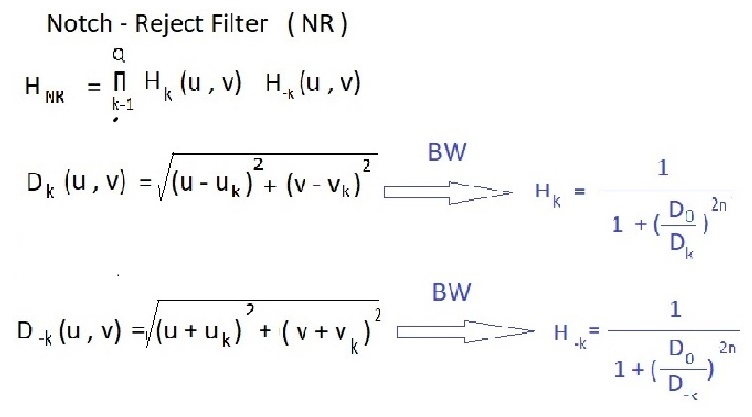
در تابع دلتای دیراک چهار عضو در محل تمرکز آن وجود دارد که عبارتند از (u , – u , -v , +v +) فقط این چهار عضو مقدار دارد .
وقتی u به uk نزدیک شود برابر 0 است اگر u به بینهایت میل کند برابر 1 است .
به معرفی فیلترهای مکانی متلب میپردازیم :
1- فیلتر Average یا میانگین کد نویسی و اجرای آن در متلب با average و نمایش آن با تابع fspecial میباشد .
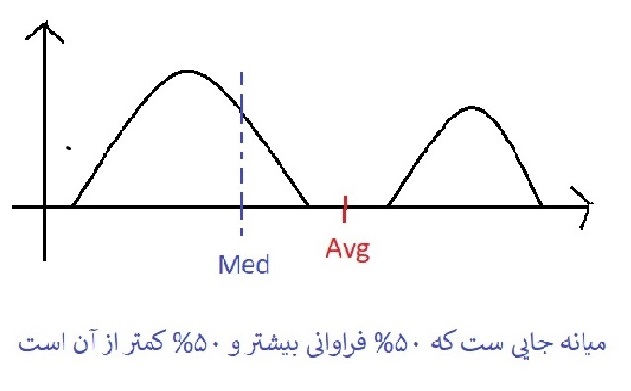
2- فیلتر Median یا میانه کد نویسی و اجرای آن در متلب با تابع medfilt2 میباشد .
3- فیلتر میانگین هندسی اجرا و کد نویسی آن در متلب با تابع colfilt میباشد .
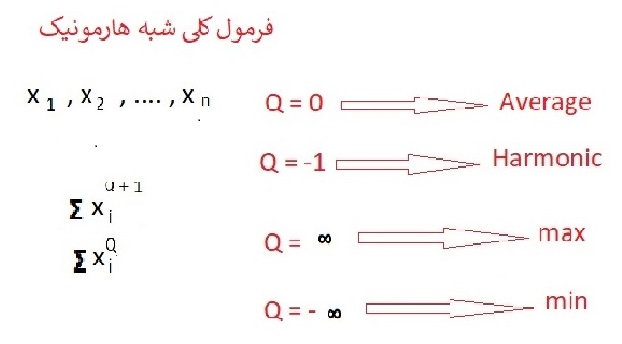
4- فیلتر میانگین توافقی یا هارمونیک که اجرا و کد نویسی آن در متلب با تابع colfilt میباشد .
5- فیلتر Contra harmonic یا شبه هارمونیک که اجرا و کد نویسی آن در متلب با تابع colfilt میباشد .
6- فیلتر Max یا بیشینه که کد نویسی و اجرای آن به عهده تابع ordfilt2 در متلب میباشد .
7- فیلتر Min یا کمینه که کد نویسی و اجرای آن به عهده تابع ordfilt2 در متلب میباشد .
8- فیلتر mid-point یا میانی که کد نویسی و اجرای آن به عهده تابع colfilt در متلب میباشد .
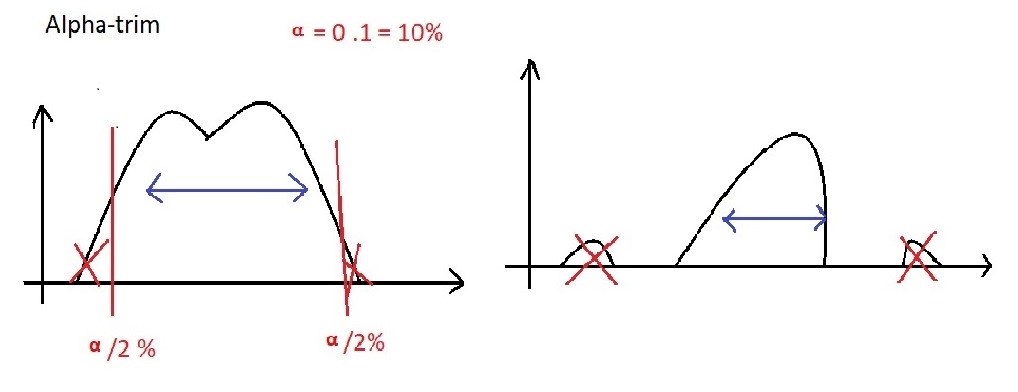
9- فیلتر Alpha – trim که کد نویسی و اجرای آن در متلب با حذف از انتها یا ابتدا صورت میگیرد .
هر کدام از این فیلترها را روی تصویر اجرا کنیم میتوانیم نویزهایی را از تصویر پاک کنیم .
از حذف نویز و فیلترینگ جهت رفع نویزهای پلاک در سیستم پلاک خوان پارکینگها جهت تشخیص پلاک خودرو بصورت هوشمند استفاده میشود که در نرم افزارهایی مانند اتوماسیون پارکینگ ، کنترل تردد خودرو مورد استفاده قرار میگیرند.
طریقه کد نویسی فیلترها در متلب :
-
function g = spatialFilter ( Type , Size , Varargin ) if nargin < 3 I I isempty ( size ) size = [3 3] ; end if nume 1 (size ) = = 1 size = [size size] ; end Type = Lower ( Type ) ; Switch Type Case ‘ median ‘ g = medfilt2 ( f , size ) ; Case { ‘ average ‘ , ‘ mean ‘ } W = fspecial ( ‘average ‘ , size ) ; G = imfilter ( f , w ) ; Case { ‘ geomtric ‘ , ‘gmean’ , ‘geomean’ , ‘ geomtricmean ‘} g = colfilt (f , size , ‘ sliding ‘ , @GeomtricMean ) ; Case { ‘ harmonic ‘ , ‘ hmean ‘ , ‘ harmean ‘ , ‘ harmonicmean ‘} g = colfilt (f , size , ‘ sliding ‘ , @ HarmonicMean) ; Case { ‘ charmonic ‘ , ‘ contraharmonic ‘} if isempty ( Varargin ) Q = 1 ; else Q = Varargin } 1 { ; end fun = @ (X) ContraHarmonicMean ( X , Q ) ; g = colfilt (f , size , ‘ sliding ‘ , fun ) ; Case ‘ max ‘ g= ordfilt2 (f , prod ( size) , true ( size ) ) ; Case ‘ min ‘ g= ordfilt2 ( f , 1 , true ( size ) ) ; Case ‘ midpoint ‘ gmin = ordfilt2 ( f , 1 , true ( size ) ) ; gmax= ordfilt2 (f , prod ( size) , true ( size ) ) ; g=( gmin + gmax ) /2 ; Case ‘ alphatrim ‘ if isempty ( Varargin ) alpha = 0 . 1 ; else alpha = Varargin } 1 { ; end fun = @ ( X ) AlphaTrimMean ( x , alpha ) ; g = colfilt ( f , size , ‘ sliding ‘ , fun ) ; Other wise Error ( ‘ Undefined filter type . ‘ ) ; end function gm= GeomtricMean (X) gm= exp (mean (Log ( X ) ) ) ; end function hm = HarmonicMean (X) hm= 1./mean (1./X) ; end function chm= ContraHarmonicMean (X) Chm= Sum ( X . ^ (Q+1) ) ./Sum( X . ^ Q ) ; end function atm = AlphaTrimMean ( X , alpha ) atm = zeros ( 1 , size ( x , 2 ) ) ; for j = 1 : nume 1 (atm ) xtj = AlphaTrim ( x ( : , j ) , alpha ) ; atm ( j ) = mean ( xtj ) ; end function xt= AlphaTrim ( X , alpha ) nx = numel ( X ) ; nt = 2*round ( alpha * nx/2 ) ; xt = sort ( X ) ; xt ( [ 1 : nt/2 end – nt/2 + 1 : end ] ) = [ ] ; end
آغاز کد نویسی با پیاده سازی فیلتر به تصویر :
-
Clc ; Clear ; Close all ; f = imread ( ‘Coins . png ‘ ) ; f = im2double ( f ) ; g = imnoise ( f , ‘ salt & pepper ‘ ) ; figure ; subplot (1, 2, 1 ) ; imshow ( f ) ; title ( ‘ Original Image ‘ ) ; subplot (1 , 2 ,2 ) ; imshow ( g ) ; title ( ‘ Noisy Image ‘ ) ;

چند نمونه نویز را به تصویر میدهیم تا بتوانیم به نتیجه بهتری در تصویر برسیم .
-
Clc ; Clear ; Close all ; f = imread ( ‘Coins . png ‘ ) ; f = im2double ( f ) ; g = imnoise ( f , ‘ salt & pepper ‘ ) ; fhat1= spatialFilter ( g , ‘median‘ , [5 5] ) ; fhat2= spatialFilter ( g , ‘ average ‘ , [5 5] ) ; fhat3= spatialFilter ( g , ‘geomtric‘ , [5 5] ) ; fhat4= spatialFilter ( g , ‘harmonic‘ , [5 5] ) ; figure ; subplot (2, 3, 1 ) ; imshow ( f ) ; title ( ‘ Original Image ‘ ) ; subplot (2, 3, 2) ; imshow (g) ; title ( ‘ Noisy Image ‘ ) ; subplot (2, 3, 3) ; imshow ( fhat 1 ) ; title ( ‘ After Meadin Filter ‘ ) ; subplot (2, 3, 4) ; imshow (fhat 2 ) ; title ( ‘ After Average Filter ‘ ) ; subplot (2, 3, 5) ; imshow (fhat 3 ) ; title ( ‘ After Geometric Mean Filter ‘ ) ; subplot (2, 3, 6 ) ; imshow (fhat 4 ) ; title ( ‘After Harmonic Mean Filter ‘ ) ;

شبیه ترین نمونه به تصویر اصلی درتابع After Meadin Filter دیده شد .
-
function gm= GeomtricMean (X) epsilon = 0.001 ; % x = max (x , epsilon ) ; x = ( 1- epsilon ) * x + epsilon ; gm= exp (mean (Log ( X ) ) ) ; end function hm = HarmonicMean (X) epsilon = 0.001 ; % x = max (x , epsilon ) ; x = ( 1- epsilon ) * x + epsilon ; hm= 1./mean (1./X) ; end Clc ; Clear ; Close all ; f = imread ( ‘Coins . png ‘ ) ; f = im2double ( f ) ; %g = imnoise ( f , ‘ Gaussian ‘ , 0 , 0.01 ) ; g = imnoise ( f , ‘ salt & pepper ‘ ) ; fhat1= spatialFilter ( g , ‘median‘ , [5 5] ) ; fhat2= spatialFilter ( g , ‘ average ‘ , [5 5] ) ; fhat3= spatialFilter ( g , ‘geomtric‘ , [5 5] ) ; fhat4= spatialFilter ( g , ‘harmonic‘ , [5 5] ) ; fhat5= spatialFilter ( g , ‘ charmonic ‘ , [5 5] , 2 ) ; fhat6= spatialFilter ( g , ‘max ‘ , [5 5] ) ; fhat7= spatialFilter ( g , ‘min ‘ , [5 5] ) ; fhat8= spatialFilter ( g , ‘ midpoint ‘ , [5 5] ) ; fhat9= spatialFilter ( g , ‘ alphatrim ‘ , [5 5] , 0.1 ) ; figure ; subplot (3, 4, 1 ) ; imshow ( f ) ; title ( ‘ Original Image ‘ ) ; subplot (3, 4, 2) ; imshow (g) ; title ( ‘ Noisy Image ‘ ) ; subplot (3, 4, 3) ; imshow ( fhat 1 ) ; title ( ‘Meadin Filter ‘ ) ; subplot (3, 4, 4) ; imshow (fhat 2 ) ; title ( ‘Average Filter ‘ ) ; subplot (3, 4, 5) ; imshow (fhat 3 ) ; title ( ‘Geometric Mean Filter ‘ ) ; subplot (3, 4, 6 ) ; imshow (fhat 4 ) ; title ( ‘Harmonic Mean Filter ‘ ) ; subplot (3, 4, 7 ) ; imshow (fhat 5 ) ; title ( ‘Contra - Harmonic Filter ‘ ) ; subplot (3, 4, 8 ) ; imshow (fhat 6 ) ; title ( ‘Max Filter ‘ ) ; subplot (3, 4, 9 ) ; imshow (fhat 7 ) ; title ( ‘ Min Filter ‘ ) ; subplot (3, 4, 10 ) ; imshow (fhat 8 ) ; title ( ‘ Mid – point Filter ‘ ) ; subplot (3, 4, 11 ) ; imshow (fhat 9 ) ; title ( ‘ \alpha – trim Filter ‘ ) ;

حالا روی تصویر اصلی نویزهای دیگر را امتحان میکنیم .
چگونگی اصلاح تصویر و تابع gaussian متلب را دنبال میکنیم .
-
g = imnoise ( f , ‘gaussian ‘ , 0 , 0.01 ) ; %g = imnoise ( f , ‘ salt & pepper ‘ ) ;