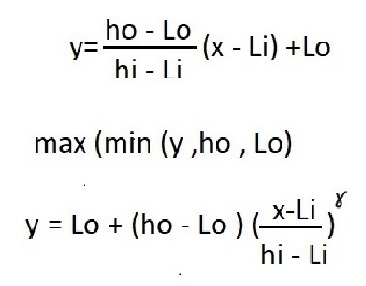تابع Imhist در تنظیم شدت نور متلب (3)

تنظیم شدت نور تصویر با تابع imadjust – enhancement – stretchlim – Imhist

در نرم افزارمتلب 

 آموزش پردازش تصویر و برنامه نویسی در متلب 3

می خوانیم :

1- تنظیم شدت نور تصویر 

2-  کار تابع imadjust

3- فرا خوانی یک تابع 

4- کار تابع enhancement

5- هیستوگرام فراوانی یک تصویر 

6- کارتابع stretchlim

7- کار تابع  Imhist

8- پراکندگی واریانس 

اینجا با تنظیم شدت نور تابع Imhist در نرم افزار متلب  آشنا میشویم .

برای وسعت دادن و بهتر کردن یک تصویر از Intensity Transforms کمک میگیریم که انجام آن را Image Enhancement گویند .

واضح تر کردن یک تصویر با نگاشت خطی اشباع در تابع imadjust صورت میگیرد .

Syntax
J=imadjust(I)
J= imadjust (I, [low- in ; high- in] ,[low-out ; high- out ])
J=imadjust(I , [low –in ; high-in], [low-out ; high- out] , gamma)
Newmap = imadjust(map , [low-in ; high- in] , [low-out ; high-out] , gamma)
RGB2 = imadjust(RGB1 , … )

 

ورودی (آی)I خروجی J (جی)  :

Low in put , high in put دو ماتریس ورودی تابع میباشند اندازه نور ورودی را با in put و اندازه نور خروجی را با out put محاسبه میکنیم

تصویر ورودی بین Low in put , high in put یک معادله خطی  lowoutput , high output  به ما میدهد .

گاما جهت منحنی را نشان میدهد اگر بزرگتر از 1 باشد منحنی رو به بالا و کوچکتر از یک باشد جهت رو به پایین است .

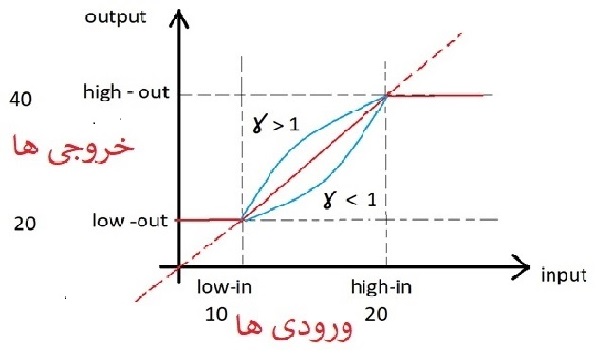
output ،  in put محدوده ورود و خروج ما را مشخص میکند .

 imread دو شاخص خروج دارد 1- خود تصویر است ، 2- کالرمپ است .

وجود تاری در تصویر نشانه نبود کنتراست به اندازه در آن است .

 اندازه بین کمترین و بیشترین روشنایی که در تصویر است کنتراست یک تصویر میگوییم .

 

 

وقتی به output ،  in put در تابع enhancement عدد ندهیم به طور اتومات میانگین سیاه و سفید تصویر را ارائه میدهد که نتیجه آن یک تصویر تار و کدر است .

هر گاه واریانس یک تصویر را بالا ببریم تمام ارکان وابسته به واریانس از جمله وضوح تصویر کنتراست آن تفاوت داده ها و پراکندگی آن بیشتر میشود به این اتفاق گسترش طیف دینامیکی یک تصویر میگوییم .

اگر یک پوشه بنام Intensity Transfrom با فایل جدید edit کنیم میتوانیم کار تابع enhancement را روی آن پیاده کنیم .

در این برنامه از  Clc برای پاک کردن صفحه ، از Clear برای پاک کردن حافظه ، از Close all برای بستن همه برنامه های در حال اجرا برنامه استفاده میکنیم .

حالا یک تصویر را پیاده سازی میکنیم .

1. %%Load Image 
   Img 1 = imread (‘pout . tif ‘) ;
   Img 2 = imadjust (img 1) ;
   %% Show Results
   Figure ;
   Subplot (1, 2, 1) ;
   Imshow (img 1) ; 
   Title (‘ Original Image ‘) ;
   Subplot (1 ,2 , 2) ;
   Imshow (img 2 ) ;
   Title (‘ Result of imadjust ‘) ;

با save کردن تصویر  و فشردن کلید F5 برنامه اجرا میشود .

 

اندازه نوری که یک تصویر دارد به مقدار کمیت آماری آن مربوط است .

ترسم نمودار فراوانی هیستوگرام تصویر اصلی  .

 

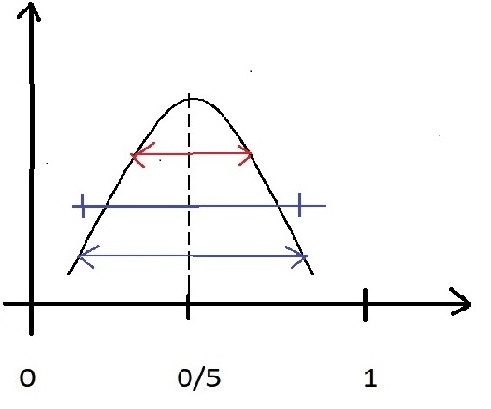
در تصویر اصلی واریانس نزدیک میانگین است که با خط قرمز در نمودار نشان داده شده در تصویر دوم واریانس واضحتر و پخشتر است که در نمودار با خط آبی نشان داده شده .

برای انتخاب بهترین حالت ممکن گرفتن img1  از خود تصویر است .

1. >>min (img 1 (:) )
   Ans =
   74 
   >>max (img 1 (:))
   Ans = 
   

   224 
   >> min (img 1 (:) ) /255
   Ans = 
   0 
   >>min (img 1 ( :) )
   Ans = 
   74 
   >> double (min (img 1 ( : ) ) ) / 255 
   Ans = 
   0/2902 
   >> double (max (img 1 ( : ) ) ) / 255 
   Ans = 
   0 /8784 
   >> 
   Img 3 = imadjust (img 1 , [0/29  0/87]  , [0 1] ) ;
    

29 صدم و 87 صدم را به جای صفر و یک قرار میدهیم .

تصویری کاملا طوسی و تار با واریانس صفر و یک .

در img1 با تابع stretchlim فراخوانی میکنیم :

1. Img3 = imadjust (img 1 , stretchlim (img 1 ) , [0 1] ) ;

 

تفاوت نامحسوسی دارد ( به تصویر اصلی میرسیم )

ببینیم در یک تصویر ضعیفتر چه میشود :

1. Img3 = imadjust (img 1 , stretchlim (img 1 ) , [0/49  0/51 ] )

 

 وقتی دو عدد را 0/5 قرار دهیم یک زمینه طوسی و کاملا تار به ما میدهد .

از پردازش تصویر در ساخت نرم افزار پلاک خوان ، راهبند هوشمند ، دستگاه پارکینگ هوشمند ، سیستم کنترل تردد خودرو و از این قبیل نرم افزارها استفاده میگردد.

1. %%Load Image 
   Img 1 = imread (‘pout . tif ‘) ;
   Img 2 = imadjust (img 1) ;
   Img3 = imadjust (img 1 , stretchlim (img 1 ) , [0 1] ) ;
   Img 4 = imadjust ( img , stretchlim ( img 1 ) , [ 0/5  0/5 ] ) ;

   

برای رسیدن به تصویر ارجینال از گرفتن میانگین وزنی ترکیب خطی تصویر 2 و 3 به آن میرسیم .

زمانی خط و منحنی با هم تفاوتی ندارند که اشباع در محدوده باشد .

 

 ارزیابی پارامترهای دیگر :

1. %%Load Image 
   Img 1 = imread (‘pout . tif ‘) ;
   Img 2 = imadjust (img 1) ;
   Img3 = imadjust (img 1 , stretchlim (img 1 ) , [0 1] ,0/5 ) ;
   Img 4 = imadjust ( img , stretchlim ( img 1 ) , [0 1] , 2 ) ;

 

 

 

 

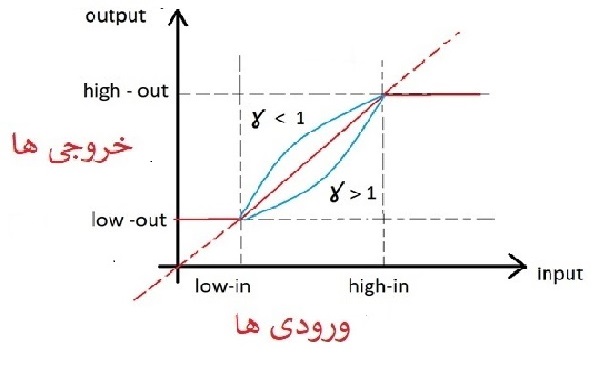
میزان تیره و روشن بودن در دو تصویر 2 و 3 کاملا واضح است .

y شیب خط  معادله خط =

در منحنی اشباع فرمول متلب توان گاما آن میشود .

در تصویر نرمال حالت خطی گاما .

تصویر3 رنگ تیره گامای بیشتر از 1 .

تصویر2 رنگ روشن گامای کمتر از 1 .

پوشش همه حالتها با گاما میسر است .

گامای  0 همان گامای کمتر از 1 است .

تابع imadjust , stretchlim کار توسعه کنتراست را به عهده دارند .

با بیشتر شدن پراکندگی واریانس تصویر وضوح بیشتری پیدا میکند .

1. >> A = magic (5)

برای تبدیل برداری یک ماتریس پنج در پنج  :

1- ریشه  A را میجوییم میشود ماتریسی با 1 سطر وهر تعداد ستون .

1. >> reshape (A , 1 , [ ] )

2- ماتریس با 1 ستون و هر تعداد سطر .

1. >>reshape (A , [ ] , 1 )

3- نمایش با بردار عمودی برای تمام اعضاء  A .

1. >> A ( : )

4- تابع  Imhist ساده ترین راه تبدیل ماتریس به بردار .

1. >>hist (img 1 ( : ) )

Error using

چون Error داد دابل میکنیم .

 

1. >> hist (double (img ( : ) ) )

در تنظیم شدت نور Imhist  نرم افزار متلب رسم اتومات نمودار توسط نرم افزار انجام میپذیرد .

 

 

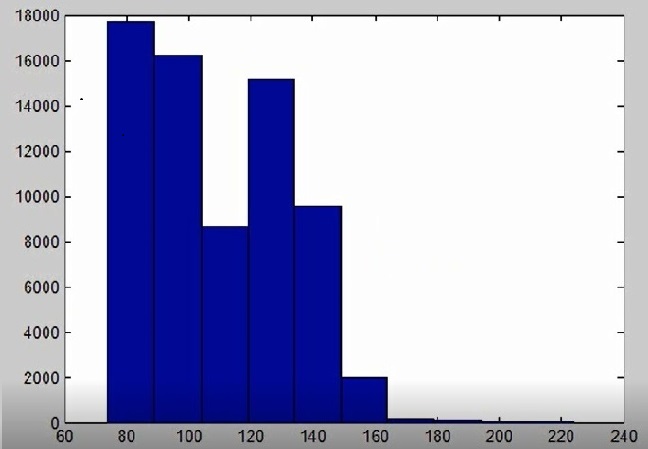
1. >> hist (double ( img 1 ( : ) ) , 50 )
   >> hist (double (img ( : ) ) , 100 )
   >> hist (double ( img 1 ( : ) ) , 256 )

 

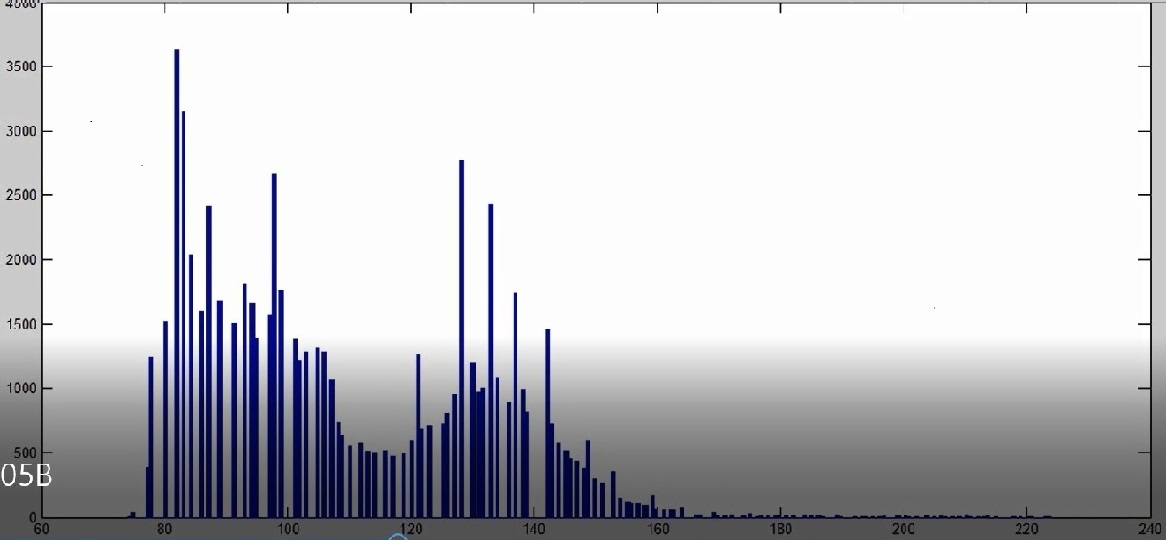
1. >> Xlim ( [ 0 255 ] )

 Imag Histogram مقدار روشنایی قسمت شده روی تصویر را نشان میدهد .

1. Imhist
   Display histogram of image data
   Syntax
   Imhist ( I )
   Imhist ( I , n )
   Imhist ( x , map )
   [counts , x ] = imhist ( … )

 ترسیم نمودار در اجرا ی سه حالت اول است .

 در یافتن مرکز دسته و تعداد اعضا دو خروجی میدهیم که ترسیم نمیشود .

برای رسم هیستوگرام هر شکل باید فیگورجدید ایجاد کنیم .

 

1. Figure ;
   Subplot ( 2 , 2 , 1 ) ;
   Imhist ( img 1 , 256 ) ;
   Title ( ‘ Original  Image ‘ ) ;
   
   Subplot ( 2 , 2 ,2) ;
   Imhist ( img 2 , 256 ) ;
   Title ( ‘ Result of imadjust ‘ ) ;
   
   Subplot ( 2 , 2 ,3) ;
   Imhist ( img 3 , 256 ) ;
   Title ( ‘ Result of imadjust  ( 2 ) ‘ ) ;
   
   Subplot ( 2 , 2 ,4 ) ;
   Imhist ( img 4 , 256 ) ;
   Title ( ‘ Result of imadjust  ( 3 ) ‘ ) ;

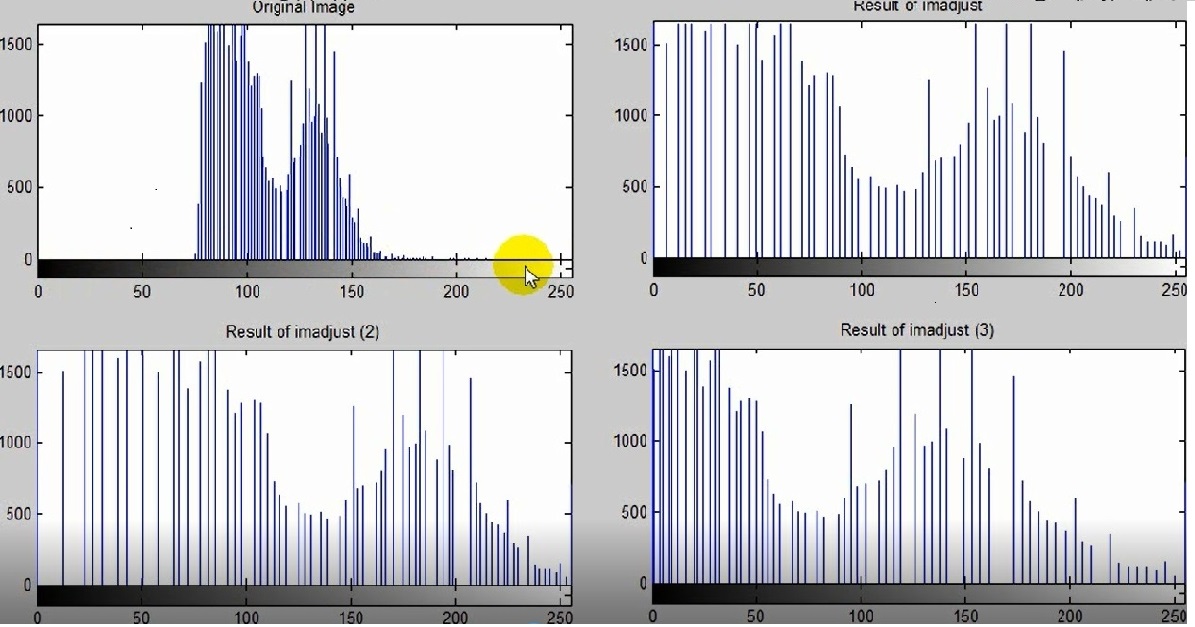
وقتی ترکیب تفکیکی زیادتری داریم که بتوانیم از همه طیف های رنگی استفاده کنیم .

 

ادامه آموزش در مبحث 4