هیستوگرا م هدف و تنظیم شدت نور متلب(4)

---

هیستوگرام هدف و تنظیم شدت نور تصویر در متلب 

 آموزش پردازش تصویر و برنامه نویسی در متلب 4

می خوانیم :

1- نمودارPDF 

2- تابع CDF 

3-  هیستوگرام هدف

4- تابع Hgram

5- تابع  adapthisteq

در هیستوگرام هدف و تنظیم شدت نور نرم افزار متلب داریم :

رسیدن به هدف آماری در هیستوگرام را آنالیز هیستوگرام گویند که در اپراتورهای خطی و غیر خطی اتفاق می افتد .

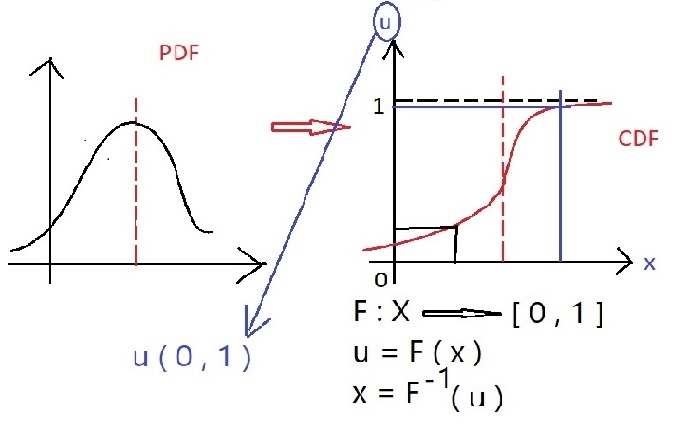
تابع کمانی احتمال یا PDF معمولا یک کمیت تصادفی را توصیف میکند .

 

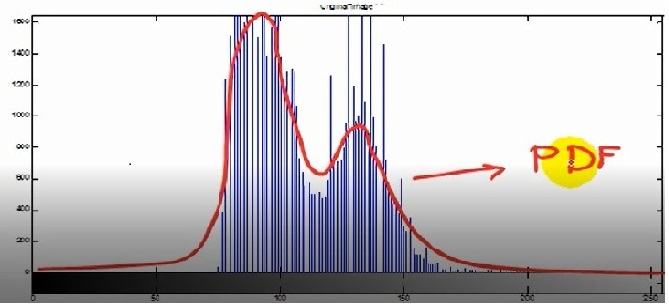
ببینیم در موارد ساده تر چگونه رفتار میکند .

 

شرط یک به یک بودن یک تابع مشتق مثبت داشتن و صعودی بودن آن است .

در تابع تجمعی احتمال یا CDF کار تناظر یک به یک بین مقادیر تصادفی در توزیع آماری پیوسته میباشد .

PDF مشتق CDF است ، زمانیCDF  صعودی است که PDF بیشتر از صفر باشد .

خط صاف را بهترین هیستوگرام تصویر میدانیم وقتی همه طیف های رنگی به طور یکنواخت باشند هیستوگرامش خطی صاف میشود .  ( در U این گونه است )

نگاشت غیر خطی تصویر = یکنواخت سازی هیستوگرام

جای  x ها ،  u ها را قرار میدهیم تا به روشنایی معادل هر  u در CDF برسیم .

در هیستوگرام کوالیزیشن نتیجه تصاویر را ببینیم :

 

1. Histeq
   Syntax
   J = histeq ( I , hgram )
   J = histeq ( I , n )
   [ J , T ] = histeq ( I  , … )
   Newmap = histeq ( X , map , hgram )
   Newmap = histeq ( X , map )
   [ newmap , T ] = histeq ( X , … )
   Img 4 = histeq ( img 1 )

2. 

 

نزدیکی لِوِلها از لحاظ یکنواختی .

نزدیک شدن به هیستوگرام خط وقتی بهینه سازی را سریع اجرا میکند .

در تصاویر پیوسته و صاف فاصله میان تابع توزیع و تولید یکنواخت کم میشود .

اختلاف با هیستوگرام مبدا را Histogram Matching حساب میکند .

 

1. I = imread ( ‘tire . tif ‘ ) ;
   J = histeq ( I ) ;
   Imshow ( I );
   Figure , imshow ( J )

 

 

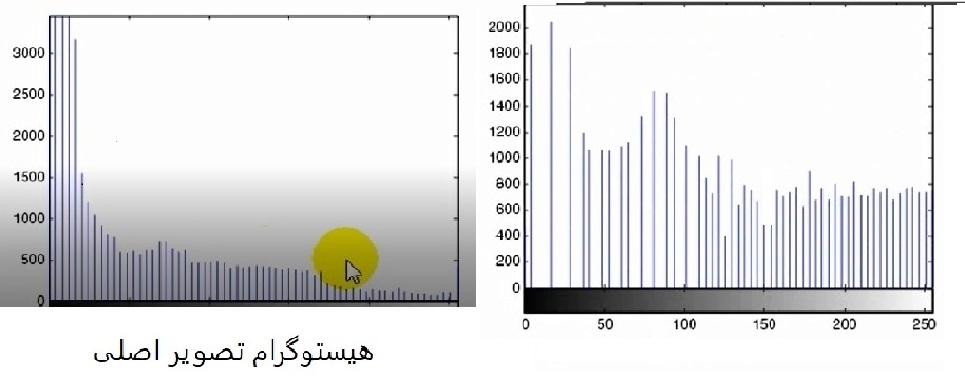
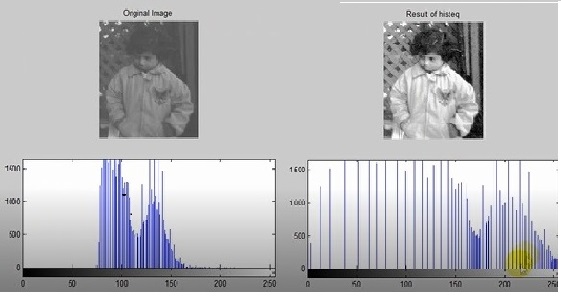
تغییر شکل در تصویر ورودی و هیستوگرام هدف در تابع histeq که کار دیگر آن یکنواخت کردن هیستوگرام است .

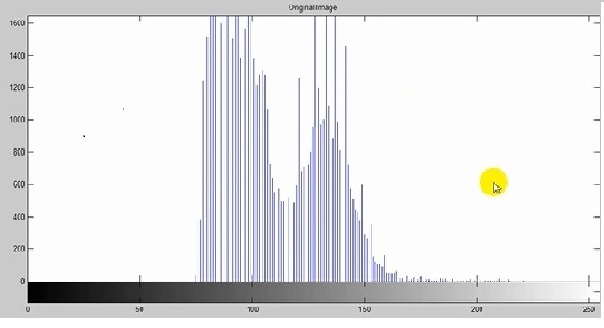
وقتی در تابع histeq هیستوگرام خروجی حاصل میشود که J = histeq ،  I = hgram است .

در تصاویر دابل در تابع hgram یونیت تصویر 8 و 256 به طور اتومات مجموع شاخصه های هیستوگرام را برابر با جمع نقاط تصویر میگیرد .

در جمع اعداد هیستوگرام باید با کمترین نقاط تصویر برابر باشد .

مجموع فراوانی کل داده ها = جمع فراوانی کل

هیستوگرام نرمال و خودکار در تابع Hgram محاسبه میشود .

 

1. %% Load Image
   Mu = 180 ;
   Sigma = 30 ;
   H=@(X) exp(-1/(2*sigma^2)*(x-mu).^2;
   X=0:255;
   Hgram=H(x);
   stem(x,hgram);
   npixel=numel(img1);
   >>size(img1)
   Ans=
   291    240
   >>291*240
   Ans=
   69840
   >>prod(size))
   Ans=
   69840

 اجرای این دستور را به مدل دیگری مینویسیم :

1. >>numel(img1)
   Ans =
   69840

جمع Hgram  و npixel حتما باید یکی شود .

 

1. Hgram= Hgram/sum(hgram);
   >>sum(hgram)
   Ans=
   1.000
   >>hgram=npixel*hgram/sun(hgram);

با فشار کلید F5 نمودار ظاهر و اعداد بزرگ میشوند .

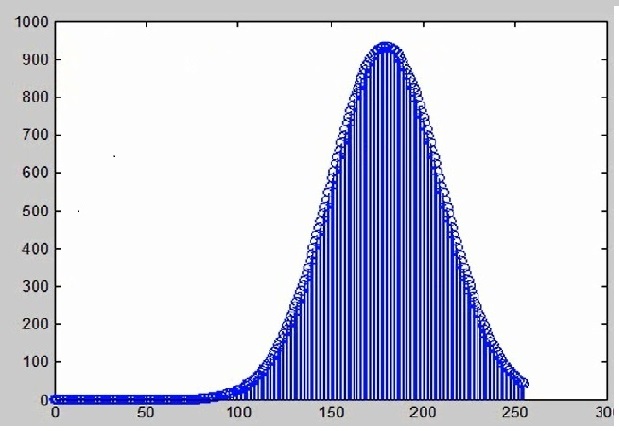
جمع اعداد را حساب میکنیم :

 

1. >>sum(hgram)
   Ans=
   6.9840e+04

 اعداد غیر صحیح است آن را رُند میکنیم .

1. >>sum(hgram) Ans= 69832 
   >>npixel Npixel= 69840

 برای نمایش هیستوگرام در هیستوگرام هدف و تنظیم شدت نور متلب :

1. Img2=histeq(img1,hgram);
    % show Results
   Figure ;
   Subplot ( 2 , 2 , 1 ) ;
   imshow ( img 1 ) ;
   title ( ‘ original Image ‘ ) ;
   subplot ( 2 , 2 , 2 ) ;
   imshow ( img 2 ) ;
   title ( ‘ Result of histeq ‘ ) ;
   subplot ( 2 , 2 , 3 ) ;
   imhist ( img 1 ) ;
   subplot ( 2 , 2 , 4 ) ;
   imhist ( img 2 ) ;

 شکل زیر نتیجه اجرای دستور بالا است .

 

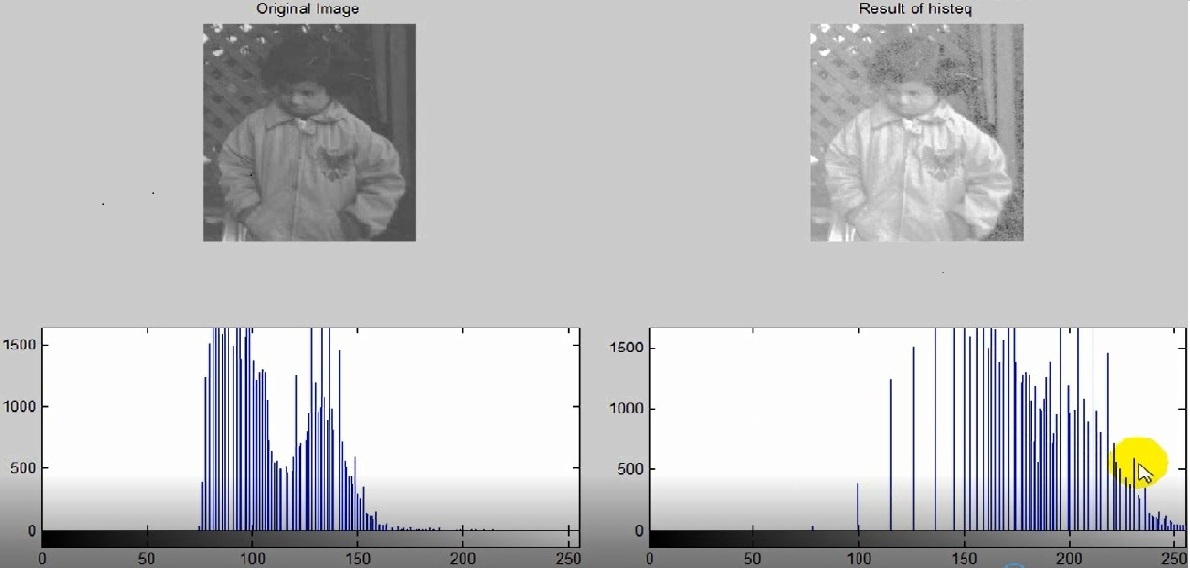
کشیدن نمودار دو قله ای :

 

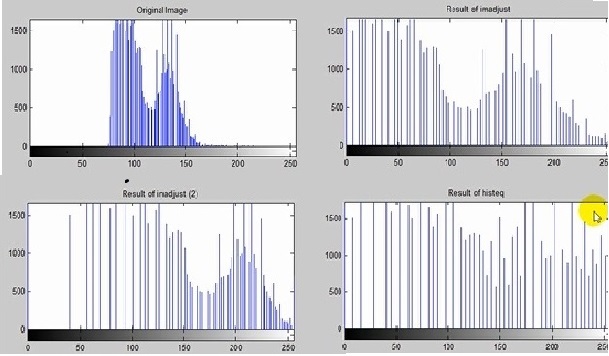
1. Img 1 imread ( ‘ pout . tif ‘ ) ;
   Npixel 1 = nume 1 ( img 1 ) ;
   W 1 = 5 ;
   Mu 1 = 50 ;
   Sigma 1 = 30 ;
   W2 = 10 ;
   Mu 2 =180 ;
   Sigma 2 = 50 ;
   H = @ ( X ) w 1 * exp ( -1 / ( 2 * sigma 1 ^ 2 ) * ( x – mu 1 ) . ^ 2 )  +w 2 * exp ( -1 / (2 * sigma 2 ^ 2 ) * (x – mu 2 ) . ^ 2 ) ;
   X = 0 : 255 ;
   Hgram = H ( x ) ;
   Hgram = round ( npixe 1 * hgram / sum ( hgram ) ) ;
   Img 2 = histeq ( img , hgram ) ;

 

 

 

 

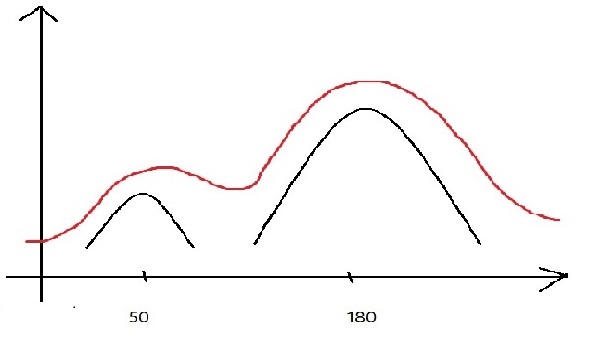
نمودار و تصویر زیر نتیجه نمودار دو قله ای بالا است .

 

در هیستوگرام هدف و تنظیم شدت نور متلب گاهی نتایج مطلوبی به دست می آوریم .

برای یافتن تفکیکی بهتر در هیستوگرام مبدا انحراف معیار تابع هدف را به الگوریتم بهینه میسپاریم و در خروجی بیشترین تفکیک پذیری را به دست می آوریم عمل در الگوریتم ژنتیک و کلاسیک به این طریق است .

لازمه هیستوگرام مچینگ دو تبدیل است :

1- هیستیکیو تبدیل به هیستوگرام یکنواخت ، 2- هیستوگرام یکنواخت به آنچه میخواهیم .

برای اشتراک گذاری با تابع توزیع احتمال ابتدا رفتار تصادفی ابجکت ها را برای هیستوگرام کوالیزیشن توصیف میکنیم  ، به این طریق خطوط تفکیک نامشخص میشود .

از پردازش تصویر در ساخت برنامه پلاک خوان برای نرم افزار کنترل تردد خودرو پارکینگ و نیز اتوماسیون پارکینگ همچنین ساخت دستگاه پارکینگ هوشمند استفاده میگردد.

این مشکل را با تابع adapthisteq از طریق عوض کردن مرزها با درون یابی خطی رفع میکنیم .

تقسیم کردن تصویر به بلوک و جدا کردن کوالیزیشن بخش ها خط های تفکیک تصویر نمایان میشود .

1. %%Load Image
   Img1 = imread ( ‘pout . tif ‘ ) ;
   Img2 = adapthisteq (img 1) ;
   %% Show Results
   Figure ;
   Subplot ( 2 , 2 , 1 );
   Imshow (img 1) ;
   Title ( ‘ Original Image ‘) ;
   Subplot ( 2 , 2 , 2);
   Imshow (img2) ;
   Title ( ‘Result of adapthisteq ‘ );

 

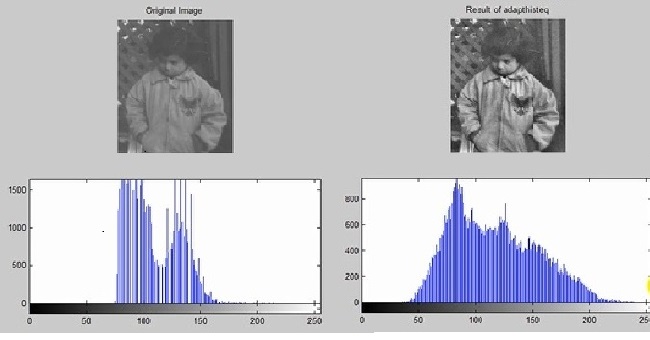
به این مکانیزم با جدا کردن بخش های مختلف تصویر میرسیم و مرکز گرایی آن با بررسی نمودارها نمایان میشود .

از بلوک های سازنده اپراتورهای خیلی بزرگ حاصل میشود .

ادامه آموزش در مبحث 5